Integrator RC merupakan jaringan RC seri terhubung yg menghasilkan sinyal output yg sinkron menggunakan proses integrasi matematika.
Untuk rangkaian integrator RC pasif, input terhubung ke hambatan sementara tegangan output diambil berdasarkan kapasitor sebagai kebalikan menurut Rangkaian Diferensiator RC. Kapasitor mengisi daya ketika input tinggi
Dalam Elektronika, rangkaian Resistor-Kapasitor (RC) seri dasar terhubung memiliki banyak kegunaan dan aplikasi mulai dari rangkaian pengisian/pengosongan dasar hingga rangkaian filter tingkat tinggi. Dua komponen rangkaian RC pasif ini mungkin terlihat cukup sederhana, tetapi tergantung pada jenis dan frekuensi sinyal input yang diterapkan, perilaku dan response dari rangkaian RC dasar ini bisa sangat berbeda.
Jaringan RC pasif tidak lebih dari sebuah resistor seri dengan kapasitor, yang merupakan resistansi tetap dalam seri dengan kapasitor yang memiliki reaktansi tergantung frekuensi yang berkurang dengan meningkatnya frekuensi lintas platnya. Jadi pada frekuensi rendah reaktansi, Xc kapasitor tinggi sedangkan pada frekuensi tinggi reaktansi rendah karena rumus reaktansi kapasitif standar Xc = 1/(2πƒC), dan kami melihat efek ini dalam tutorial kami tentang Low Pass Filter Pasif.
Jika sinyal input adalah gelombang sinusoidal, integrator RC hanya akan bertindak sebagai low pass filter (LPF) sederhana di atas titik cut-off dengan frekuensi cut-off atau sudut yang sesuai dengan konstanta waktu RC (tau, τ ) dari jaringan seri. Jadi ketika diumpankan dengan gelombang sinusoidal murni, integrator RC bertindak sebagai low pass filter pasif yang mengurangi outputnya di atas titik frekuensi cut-off.
Seperti yang telah kita lihat sebelumnya, konstanta waktu RC mencerminkan hubungan antara resistansi dan kapasitansi terhadap waktu dengan jumlah waktu, diberikan dalam detik, berbanding lurus dengan resistansi, R dan kapasitansi, C.
Dengan demikian laju pengisian atau pengosongan tergantung pada konstanta waktu RC, τ = RC. Pertimbangkan rangkaian di bawah ini.
Rangkaian Integrator RC (Resistor-Kapasitor)

Untuk rangkaian integrator RC, sinyal input diterapkan pada resistor dengan output diambil pada kapasitor, maka VOUT sama VC. Karena kapasitor adalah elemen yang tergantung pada frekuensi, jumlah muatan yang dipasang melintasi plat sama dengan integral domain waktu dari arus. Itu membutuhkan sejumlah waktu untuk kapasitor untuk mengisi penuh karena kapasitor tidak dapat mengisi secara instan hanya mengisi secara eksponensial.
Oleh karena itu arus kapasitor dapat ditulis sebagai:

Persamaan dasar di atas dari iC = C (dVc/dt) juga dapat dinyatakan sebagai tingkat perubahan muatan sesaat, Q sehubungan dengan waktu memberi kita persamaan standar berikut: iC = dQ/dt di mana muatan Q = C x Vc, yaitu kapasitansi kali tegangan.
Tingkat di mana kapasitor mengisi (atau melepaskan) berbanding lurus dengan jumlah resistansi dan kapasitansi yang memberikan konstanta waktu dari rangkaian. Jadi konstanta waktu dari rangkaian integrator RC adalah interval waktu yang sama dengan hasil R dan C.
Karena kapasitansi sama dengan Q/Vc di mana muatan listrik, Q adalah aliran arus (i) dari waktu ke waktu (t), itu adalah hasil dari (i x t) dalam coulomb, dan dari hukum Ohm kita tahu bahwa tegangan (V) sama dengan untuk (i x R), menggantikan ini ke dalam persamaan untuk konstanta waktu RC memberikan:
Konstanta Waktu RC (Time Constant RC)

Kemudian kita dapat melihat bahwa karena i dan R batal, hanya T yang tetap yang menunjukkan bahwa konstanta waktu dari rangkaian integrator RC memiliki dimensi waktu dalam detik, diberikan huruf Yunani tau, τ. Perhatikan bahwa konstanta waktu ini mencerminkan waktu (dalam detik) yang diperlukan kapasitor untuk mengisi hingga 63.2% dari tegangan maksimum atau pelepasan ke 36.8% dari tegangan maksimum.
Tegangan Kapasitor

Kami mengatakan sebelumnya bahwa untuk integrator RC, output adalah sama dengan tegangan kapasitor, yang: VOUT sama VC. Tegangan ini sebanding dengan muatan, Q disimpan pada kapasitor yang diberikan oleh: Q = VxC.
Hasilnya adalah bahwa tegangan output adalah bagian integral dari tegangan input dengan jumlah integrasi tergantung pada nilai-nilai R dan C dan karenanya konstanta waktu jaringan.
Kami melihat di atas bahwa arus kapasitor dapat dinyatakan sebagai laju perubahan muatan, Q sehubungan dengan waktu. Oleh karena itu, dari aturan dasar kalkulus differensial, turunan dari Q sehubungan dengan waktu adalah dQ/dt dan karena i = dQ/dt kita mendapatkan hubungan berikut:
Q = ∫idt (muatan Q pada kapasitor setiap saat)
Karena input terhubung ke resistor, arus yang sama, i harus melewati resistor dan kapasitor (iR = iC ) menghasilkan penurunan tegangan VR di resistor sehingga arus, (i) mengalir melalui Jaringan RC seri ini diberikan sebagai:

Oleh karena itu:

Ketika i = VIN/R, mengganti dan mengatur ulang untuk menyelesaikan untuk VOUT sebagai fungsi waktu menghasilkan:

Jadi dengan kata lain, output dari rangkaian integrator RC, yang merupakan tegangan melintasi kapasitor sama dengan waktu Integral dari tegangan input, VIN tertimbang oleh konstanta 1/RC. Di mana RC mewakili konstanta waktu, τ.
Kemudian dengan asumsi muatan awal pada kapasitor adalah nol, yaitu VOUT = 0, dan tegangan input VIN adalah konstan, tegangan output, VOUT dinyatakan dalam domain waktu sebagai:
Rumus Integrator RC (Resistor-Kapasitor)

Jadi rangkaian integrator RC adalah salah satu di mana tegangan output, VOUT sebanding dengan integral dari tegangan input, dan dengan ini, mari kita lihat apa yang terjadi ketika kita menerapkan pulsa positif tunggal dalam bentuk tegangan step ke rangkaian integrator RC.
Integrator RC Pulsa Tunggal
Ketika pulsa tegangan satu langkah diterapkan ke input integrator RC, kapasitor mengisi melalui resistor sebagai respons terhadap pulsa. Namun, output tidak instan karena tegangan melintasi kapasitor tidak dapat berubah secara instan tetapi meningkat secara eksponensial ketika kapasitor mengisi pada tingkat yang ditentukan oleh konstanta waktu RC, τ = RC.
Kita sekarang tahu bahwa laju di mana kapasitor baik mengisi atau melepaskan ditentukan oleh konstanta waktu RC dari rangkaian. Jika pulsa tegangan step yang ideal diterapkan, yaitu dengan lonjakan terdepan dan lonjakan belakang dianggap instan, tegangan melintasi kapasitor akan meningkat untuk pengisian dan penurunan untuk pemakaian, secara eksponensial dari waktu ke waktu pada kecepatan yang ditentukan oleh:
Pengisian Kapasitor

Pengosongan Kapasitor

Jadi jika kita mengasumsikan tegangan kapasitor satu volt (1V), kita dapat memplot persentase pengisian atau pengosongan kapasitor untuk setiap konstanta waktu R individu seperti yang ditunjukkan pada tabel berikut.
Konstanta
Waktu
Pengisian
Kapasitor
Pengosongan
Kapasitor
Τ
% Mengisi
% Melepas
0.5
39.4%
60.6%
0.7
50%
50%
1
63.2%
36.7%
2
86.4%
13.5%
3
95.0%
4.9%
4
98.1%
1.8%
5
99.3%
0.67%
Perhatikan bahwa pada konstanta 5 kali atau lebih, kapasitor dianggap 100 persen terisi penuh atau habis penuh. Jadi sekarang mari kita asumsikan kita memiliki rangkaian integrator RC yang terdiri dari resistor 100kΩ dan kapasitor 1uF seperti yang ditunjukkan.
Contoh: Rangkaian Integrator RC No.1

Konstanta waktu, τ dari rangkaian integrator RC oleh karena itu diberikan sebagai:
RC = 100kΩ x 1uF = 100ms.
Jadi jika kita menerapkan pulsa tegangan step ke input dengan durasi katakanlah, dua konstanta waktu (200mS), maka dari tabel di atas kita dapat melihat bahwa kapasitor akan mengisi daya hingga 86.4% dari nilai terisi penuh. Jika pulsa ini memiliki amplitudo 10 volt, maka ini sama dengan 8.64 volt sebelum kapasitor dilepaskan kembali melalui resistor ke sumber saat pulsa input kembali ke nol.
Jika kita mengasumsikan bahwa kapasitor dibolehkan untuk melepaskan penuh dalam waktu 5 konstanta waktu, atau 500mS sebelum kedatangan pulsa input berikutnya, maka grafik kurva pengisian dan pengosongan akan terlihat seperti ini:
Kurva Pengisian/Pengosongan Integrator RC

Perhatikan bahwa kapasitor mengeluarkan dari nilai awal 8.64 volt (2 konstanta waktu) dan bukan dari input 10 volt.
Kemudian kita dapat melihat bahwa ketika konstanta waktu RC diperbaiki, setiap variasi pada lebar pulsa input akan mempengaruhi output dari rangkaian integrator RC. Jika lebar pulsa meningkat dan sama dengan atau lebih besar dari 5RC, maka bentuk pulsa output akan sama dengan input karena tegangan output mencapai nilai yang sama dengan input.
Namun jika lebar pulsa berkurang di bawah 5RC, kapasitor hanya akan mengisi sebagian dan tidak mencapai tegangan input maksimum yang menghasilkan tegangan output lebih kecil karena kapasitor tidak dapat mengisi sebanyak yang mengakibatkan tegangan output yang sebanding dengan integral input tegangan.
Jadi jika kita mengasumsikan pulsa input sama dengan satu konstanta waktu, yaitu 1RC, kapasitor akan mengisi dan mengosongkan tidak antara 0 volt dan 10 volt tetapi antara 63.2% dan 3807% dari tegangan melintasi kapasitor pada saat perubahan. Perhatikan bahwa nilai-nilai ini ditentukan oleh konstanta waktu RC.
Konstanta Waktu Perbaikan Integrator RC
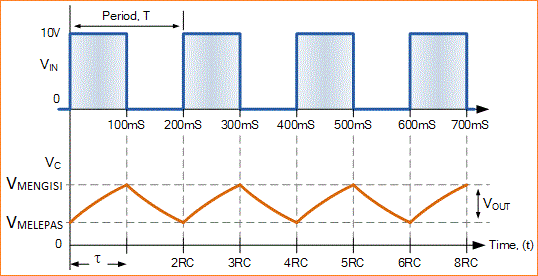
Jadi untuk input pulsa kontinu, hubungan yang benar antara waktu periodik input dan konstanta waktu RC dari rangkaian, integrasi input akan berlangsung menghasilkan semacam ramp up, dan kemudian ramp down output. Tetapi agar rangkaian berfungsi dengan benar sebagai integrator, nilai konstanta waktu RC harus besar dibandingkan dengan input waktu periodik. Itu adalah RC ≫ T, biasanya 10 kali lebih besar.
Ini berarti bahwa besarnya tegangan output (yang sebanding dengan 1/RC) akan sangat kecil antara tegangan tinggi dan rendahnya sangat melemahkan tegangan output. Ini karena kapasitor memiliki lebih sedikit waktu untuk mengisi dan mengosongkan antara pulsa tetapi tegangan DC output rata-rata akan meningkat menuju satu setengah besarnya input dan dalam contoh pulsa kami di atas, ini akan menjadi 5 volt (10/2).
Integrator RC sebagai Generator Gelombang Sinus
Kita telah melihat di atas bahwa rangkaian integrator RC dapat melakukan operasi integrasi dengan menerapkan input pulsa yang menghasilkan output gelombang segitiga ramp-up dan ramp-down karena karakteristik pengisian dan pengosongan kapasitor. Tetapi apa yang akan terjadi jika kita membalikkan proses dan menerapkan bentuk gelombang segitiga ke input, apakah kita akan mendapatkan output gelombang atau pulsa persegi?
Ketika sinyal input ke rangkaian integrator RC adalah input berbentuk pulsa, outputnya adalah gelombang segitiga. Tetapi ketika kita menerapkan gelombang segitiga, output menjadi gelombang sinus karena integrasi dari waktu ke waktu sinyal ramp.
Ada banyak cara untuk menghasilkan bentuk gelombang sinusoidal, tetapi satu cara sederhana dan murah untuk secara elektronik menghasilkan bentuk gelombang jenis gelombang sinus adalah dengan menggunakan sepasang rangkaian integrator RC pasif yang dihubungkan bersama secara seri seperti yang ditunjukkan.
Gelombang Sinus Integrator RC

Di sini integrator RC pertama mengubah input berbentuk pulsa asli menjadi gelombang segitiga ramp-up dan ramp-down yang menjadi input integrator RC kedua. Rangkaian integrator RC kedua ini membulatkan titik-titik gelombang segitiga mengubahnya menjadi gelombang sinus karena secara efektif menjalankan integrasi ganda pada sinyal input asli dengan konstanta waktu RC yang mempengaruhi tingkat integrasi.
Ketika integrasi ramp menghasilkan fungsi sinus, (pada dasarnya bentuk gelombang segitiga-off) frekuensi periodiknya di Hertz akan sama dengan periode T dari pulsa asli. Perhatikan juga bahwa jika kita membalikkan sinyal ini dan sinyal input adalah gelombang sinusoidal, rangkaian tidak bertindak sebagai integrator, tetapi sebagai low pass filter (LPF) sederhana dengan gelombang sinusoidal, menjadi gelombang murni tidak berubah bentuk, hanya amplitudo yang terpengaruh.
Ringkasan Integrator RC (Resistor-Kapasitor)
Kita telah melihat di sini bahwa integrator RC pada dasarnya adalah rangkaian low-pass filter seri RC yang ketika pulsa tegangan langkah diterapkan pada inputnya menghasilkan output yang sebanding dengan integral inputnya. Ini menghasilkan persamaan standar: Vo = ∫Vi dt di mana Vi adalah sinyal yang diumpankan ke integrator dan Vo adalah sinyal output terintegrasi.
Integrasi fungsi langkah input menghasilkan output yang menyerupai fungsi ramp segitiga dengan amplitudo lebih kecil daripada input pulsa asli dengan jumlah redaman yang ditentukan oleh konstanta waktu. Dengan demikian bentuk gelombang output tergantung pada hubungan antara konstanta waktu dari rangkaian dan frekuensi (periode) dari pulsa input.
Konstanta waktu integrator RC selalu dibandingkan dengan periode, T dari input, sehingga konstanta waktu RC yang panjang akan menghasilkan bentuk gelombang segitiga dengan amplitudo rendah dibandingkan dengan sinyal input karena kapasitor memiliki lebih sedikit waktu untuk mengisi atau mengeluarkan penuh. Konstanta waktu yang singkat memungkinkan kapasitor lebih banyak waktu untuk mengisi dan mengeluarkan, menghasilkan bentuk bulat yang lebih khas.
Dengan menghubungkan dua rangkaian integrator RC secara paralel memiliki efek integrasi ganda pada pulsa input. Hasil dari integrasi ganda ini adalah bahwa rangkaian integrator pertama mengubah pulsa tegangan step menjadi bentuk gelombang segitiga dan rangkaian integrator kedua mengubah bentuk gelombang segitiga dengan membulatkan titik-titik dari bentuk gelombang segitiga menghasilkan bentuk gelombang output gelombang sinus dengan sangat berkurang amplitudo.






0 Komentar